Далее идут мои небольшие заметки по линейной алгебре, применяемой в компьютерной графике.
Линейные комбинации
Для множества векторов \(S = \{v_1, v_2, \dots, v_n\}\) линейной комбинацией называется выражение вида:
\(v = \alpha_1 v_1 + \alpha_2 v_2 + \dots + \alpha_n v_n\), где
\(\alpha_n\) - произвольные скаляры.
Базисные векторы
Базисом векторного пространства называется множество линейно независимых векторов, все линейные комбинации которых образуют данное пространство, т.е. любой вектор, принадлежащий этому пространству можно выразить через единственно возможную линейную комбинацию векторов, входящих в базис. Векторы, входящие в базис, называются базис векторами. Для одного и того же векторного пространства существует бесконечное количество базисов, но во всех из них содержится одинаковое количество векторов.
Стандартным базисом пространства \(\mathbb{R}^n\) называется множество векторов вида:
\[\begin{cases} e_1 = \left(1, 0, \dots, 0\right)\\ e_2 = \left(0, 1, \dots, 0\right)\\ \dots\\ e_n = \left(0, 0, \dots, 1\right) \end{cases}\]
Скалярное произведение
\(\alpha = v \cdot w = v_x w_x + v_y w_y + v_z w_z = \|v\|\|w\|\cos\left(\theta\right)\), где:
- \(\theta\) — угол между векторами \(v\) и \(w\).
Векторное произведение
\(u = v \times w = \left(v_y w_z - w_y v_z, v_z w_x - w_z v_x, v_x w_y - w_x v_y \right)\)
Векторным произведеним двух векторов \(v\) и \(w\) в пространстве \(\mathbb{R}^3\) называется вектор \(u\), удовлетворяющий следующим свойствам:
- \(u\) перпендикулярен \(v\) и \(w\);
- \(u\) имеет длину равную площади параллелограмма, образуемого \(v\) и \(w\): \(\| u \| = \| v \| \| w \| \sin \theta\), где \(\theta\) — угол между векторами \(v\) и \(w\);
- направление \(u\) определяется по правилу правой руки: нужно направить указательный палец вдоль \(v\), средний — вдоль \(w\), направление \(u\) будет соответствовать направлению большого пальца.
Свойства векторного произведения:
- \(v \times w = -\left(w \times v\right)\).
- \(u \times \left(v + w\right) = \left(u \times v\right) + \left(u \times w\right)\).
- \(\left(u + v\right) \times w = \left(u \times w\right) + \left(v \times w \right)\).
- \(\alpha \left(v \times w\right) = \left(\alpha v\right) \times w = v \times \left(\alpha w\right)\).
- \(v \times 0 = 0 \times v = 0\).
- \(v \times v = 0\).
Линейное отображение
Линейным отображением векторного пространства \(V\) в векторное пространство \(W\) называется отображение:
\(f \colon V \to W\), удовлетворяющее свойствам линейности:
- \(f\left(v_1 + v_2\right) = f\left(v_1\right) + f\left(v_2\right)\).
- \(f\left(\alpha v_1\right) = \alpha f\left(v_1\right)\).
Связь с базисными векторами
Вспомним, что любой вектор \(v \in V\) можно представить, как линейную комбинацию базисных векторов: \(v = \alpha_1 v_1 + \alpha_2 v_2 + \dots + \alpha_n v_n\), где
\(\{v_1, v_2, \dots, v_n\}\) — базис пространства \(V\).
Далее рассмотрим применение линейного отображения \(f \colon V \to W\) к произвольному вектору \(v\).
\[\begin{equation} \begin{split} f\left(v\right) & = f\left(x_1 v_1 + x_2 v_2 + \dots + x_n v_n\right) \\ & = x_1 f\left(v_1\right) + x_2 f\left(v_2\right) + \dots + x_n f\left(v_n\right) \end{split} \end{equation}\]
Мы пришли к линейной комбинации с изначальными компонентами \(\alpha\), но с изменёнными базисными векторами. Таким образом, получив отображение базисных векторов, мы можем получить отображение произвольного вектора, используя только его компоненты \(\alpha\). Разовьём эту идею дальше, каждый базисный вектор \(v_i \in V\) мы можем представить как линейную комбинацию базисных векторов \(w_i \in W\).
\(f\left(v_i\right) = \alpha_{1,i} w_1 + \alpha_{2,i} w_2 + \dots + \alpha_{n,i} w_n\)
Так как мы использовуем стандартный базис \(W\), предыдущее выражение сокращается до:
\(f\left(v_i\right) = \left(\alpha_{1,i}, \alpha_{2,i}, \dots, \alpha_{n,i}\right)\)
Совмещая вышенаписанные уравнения, получим:
\[ \begin{align} f\left(v\right) & = x_1 \left(\alpha_{1,1}, \alpha_{2,1}, \dots, \alpha_{m,1}\right) \\ & + x_2 \left(\alpha_{1,2}, \alpha_{2,2}, \dots, \alpha_{m,2}\right) \\ &\;\;\vdots \\ & + x_n \left(\alpha_{1,n}, \alpha_{2,n}, \dots, \alpha_{m,n}\right) \end{align} \]
Таким образом, мы можем заранее рассчитать и сохранить коэффициенты \(\alpha_{i,j}\), чтобы потом с их помощью отображать любой вектор \(v \in V\) в пространство \(W\).
В виду данного свойства можно представить отображение в виде матрицы \(n \times m\):
\(f(v) = Av\)
\[ f\left(v\right) = \begin{pmatrix} \alpha_{1,1} & \alpha_{2,1} & \dots & \alpha_{m,1} \\ \alpha_{1,2} & \alpha_{2,2} & \dots & \alpha_{m,2} \\ \vdots \\ \alpha_{1,n} & \alpha_{2,n} & \dots & \alpha_{m,n} \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \]
Матрицы в OpenGL
Для загрузки матриц в OpenGL используется процедура
void glUniformMatrix4fv(
GLint location,
GLsizei count,
GLboolean transpose,
const GLfloat *value
);Если transpose = GL_FALSE, матрица не будет транспонирована, а будет загружена в память
как есть. Но в OpenGL используются столбцовые матрицы, это значит, что при загрузке
следующей матрицы с параметром transpose = GL_FALSE
\[ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{pmatrix} \]
Она будет интерпретироваться, как её транспонированная версия (хотя само транспонирование произведено не будет)
\[ \begin{pmatrix} 1 & 5 & 9 & 13 \\ 2 & 6 & 10 & 14 \\ 3 & 7 & 11 & 15 \\ 4 & 8 & 12 & 16 \end{pmatrix} \]
Поэтому при написании кода для умножения матрицы на матрицу, надо использовать не привычный порядок “строка на столбец”, а порядок “столбец на строку”. При этом хранить все элементы матрицы надо тоже в транспонированном виде, т.е. массив, в котором будет хранится вышеописанная матрица будет иметь вид:
typedef float mat4_t[16]; // матрица 4x4
mat4_t m1 = {
1.f, 5.f, 9.f, 13.f,
2.f, 6.f, 10.f, 14.f,
3.f, 7.f, 11.f, 15.f,
4.f, 8.f, 12.f, 16.f,
};Аффинные преобразования
Аффинные преобразования, в отличие от линейных, можно применять и к векторам и к точкам (т.е. к элементам аффинного пространства). В общем виде аффинное преобразование имеет вид:
\(Ax + y\), где:
- \(A\) — матрица \(n \times m\),
- \(y\) — \(m\) вектор.
Его также можно представить в виде умножения матрицы на вектор:
\[ \begin{pmatrix} A & y \\ 0^T & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ 1 \end{pmatrix} = \begin{pmatrix} Ax + y \\ 1 \end{pmatrix} \]
Преобразование нормалей
Рассмотрим уравнение плоскости, заданной нормалью:
\(ax + by + cz + d = 0\)
Представим левую часть в виде произведения векторов:
\[ \begin{pmatrix} a & b & c & d \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = n^T P \]
Если применить аффинное преобразование \(A\) ко всем точкам плоскости, получим:
\(\left(Bn\right)^T \left(AP\right)\), где \(B\) — соответствующее аффинное преобразование нормали.
С помощью следующих проебразований уравнения получим:
\[ \begin{align} \left(Bn\right)^T \left(AP\right) & = 0 \\ n^T B^T A P & = 0 \end{align} \]
Одним из решений уравнения является
\[ \begin{align} I & = B^T A \\ B & = (A^{-1})^T \end{align} \]
Отсюда выходит, что преобразованная нормаль равна:
\(n' = (A^{-1})^T n\)
Камера
Камера определяется позицией, направлением взгляда и направлением вектора, указывающего наверх.
mat4 lookat_mat(
vec3 pos, // позиция камеры
vec3 lookat, // точка, в которую направлена камера
vec3 up // вектор, указывающий наверх (нормализованный)
);Для построения преобразования координат камеры в мировые координаты, нам нужны базисные векторы пространства камеры. Для начала получим вектор направления взгляда (направлен вдоль оси z). Мы вычитаем точку \(lookat\) из точки \(pos\), т.к. в OpenGL ось z направлена от экрана в даль, а нам бы хотелось сделать так, чтобы вдаль устремлялось положительное направление оси z:
\(\hat{v}_{dir} = \frac{pos - lookat}{\|pos - lookat\|}\)
Далее получим вектор, направленный в сторону (вдоль x):
\(\hat{v}_{side} = \hat{v}_{dir} \times \hat{up}\)
И, наконец, получим вектор, направленный вверх:
\(\hat{v}_{up} = \hat{v}_{side} \times \hat{v}_{dir}\)
При написании кода важно производить нормализацию всех вышеперечисленных векторов. Хоть векторное произведение и должно давать нормализованный вектор, если оба его операнда нормализованные, но из-за погрешностей не всегда происходит именно так.
Теперь построим преобразование из координат камеры в мировые координаты:
\[ M_{view \to world} = \begin{pmatrix} \hat{v}_{side} & \hat{v}_{up} & \hat{v}_{dir} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 & pos_x \\ 0 & 1 & 0 & pos_y \\ 0 & 0 & 1 & pos_z \\ 0 & 0 & 0 & 1 \end{pmatrix} \]
Осталось только инвертировать данное преобразование. Как можно заметить, первая матрица является матрицей вращения, для её инверсии нужно произвести транспонирование. Вторая матрица является матрицей смещения, для её инверсии нужно изменить знак у шагов смещения по разным координатным осям:
\[ M_{world \to view} = \begin{pmatrix} \hat{v}_{side}^T & 0 \\ \hat{v}_{up}^T & 0 \\ \hat{v}_{dir}^T & 0 \\ 0^T & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 & -pos_x \\ 0 & 1 & 0 & -pos_y \\ 0 & 0 & 1 & -pos_z \\ 0 & 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} \hat{v}_{side}^T & -\hat{v}_{side} \cdot pos \\ \hat{v}_{up}^T & -\hat{v}_{up} \cdot pos \\ \hat{v}_{dir}^T & -\hat{v}_{dir} \cdot pos \\ 0^T & 1 \end{pmatrix} \]
Перспективная проекция
Каждая точка 3D пространства усекается с помощью пирамиды, затем получившаяся точка переводится в нормализованные экранные координаты. Пирамида задаётся четырьма параметрами:
- \(aspect = \frac{width}{height}\) — отношение ширины окна к высоте,
- \(fovy\) — угол поля зрения по \(y\),
- \(z_n\) — расстояние от начала координат до ближней плоскости отсечения,
- \(z_f\) — расстояние от начала координат до дальней плоскости отсечения.
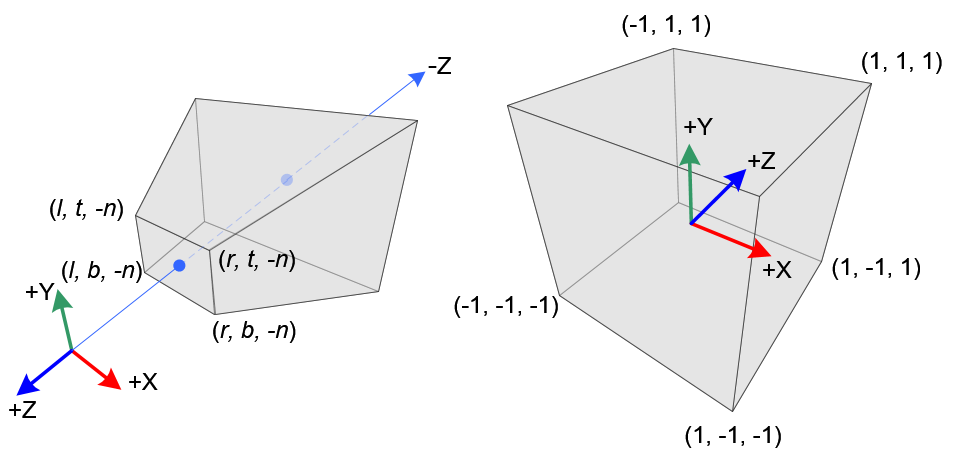
Нужно учитывать, что в OpenGL система нормализованных экранных координат является левой, а система мировых координат и координат вида — правой.
Расмотрим проецирование на плоскостях YZ и XZ:
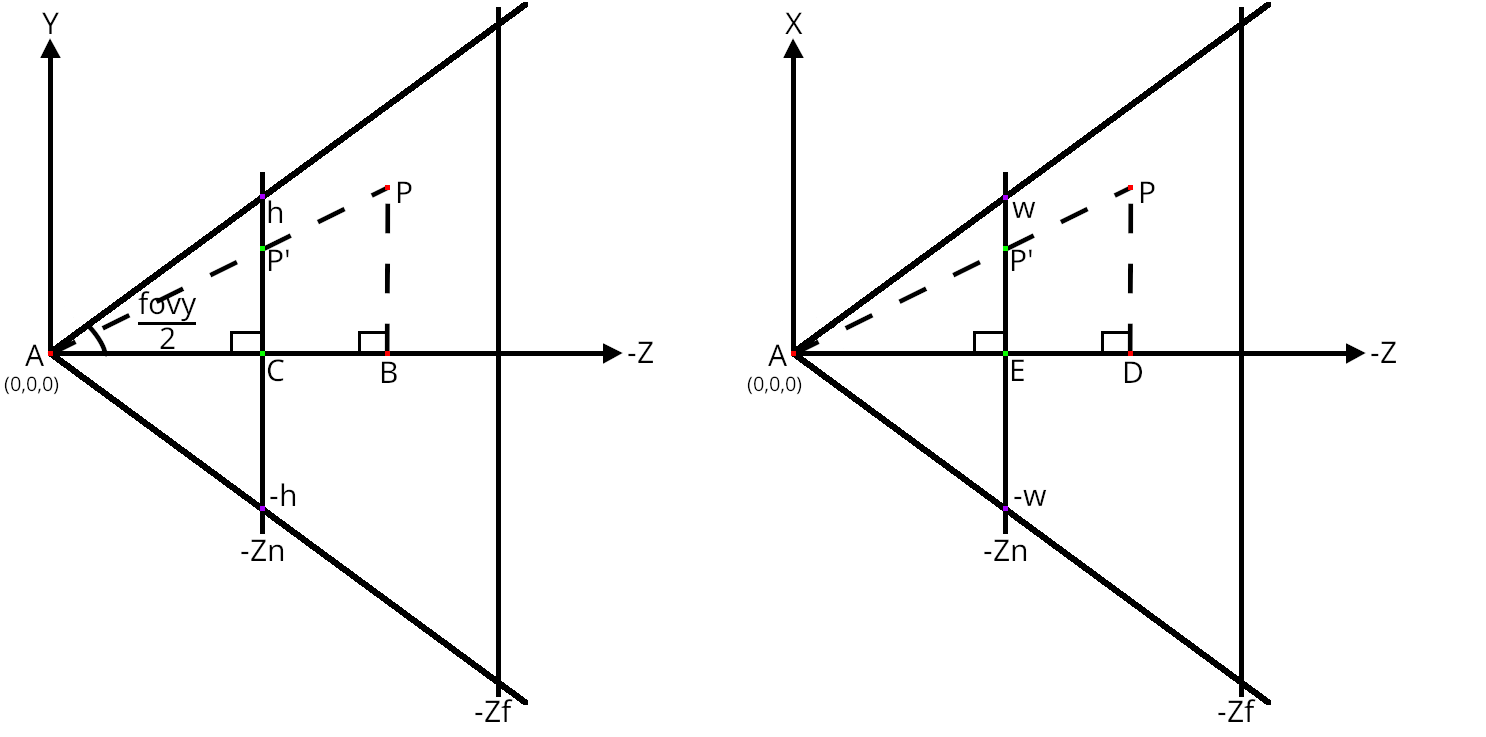
Как видно на рисунке, мы проецируем точку \(P\), координаты проекции точки обозначены \(P'\). Рассмотрим прямоугольные треугольники \(APB\) и \(AP'C\). Они подобны по первому признаку: \(\angle{PAB} = \angle{P'AC}\) и \(\angle{P'CA} = \angle{PBA}\). Из чего следует следующее равенство: \(\frac{P'C}{PB} = \frac{CA}{BA}\) или, что тоже самое, \(\frac{P'_y}{P_y} = \frac{P'_z}{P_z} = \frac{z_n}{-P_z}\). Выводим из этого равенства \(P'_y\): \(P'_y = P_y \frac{z_n}{-P_z}\).
Далее рассмотрим плоскость XZ, прямоугольные треугольники \(P'AE\) и \(PAD\) подобны по первому признаку. Из чего следует равенство \(\frac{P'E}{PD} = \frac{EA}{DA}\) или, что тоже самое, \(\frac{P'_x}{P_x} = \frac{z_n}{-P_z}\). Выводим из этого равенства \(P'_x = P_x \frac{z_n}{-P_z}\).
Таким образом мы получили все координаты проекции: \(P' = \left(P_x \frac{z_n}{-P_z}, P_y \frac{z_n}{-P_z}, -z_n\right)\). Как можно видеть, координаты \(P'_x\) и \(P'_y\) обратно пропорциональны координате \(P_z\). Чем дальше \(P_z\) от плоскости \(z_n\), тем меньше будут координаты \(P'_x\) и \(P'_y\).
Запишем промежуточную матрицу проекции (далее мы добавим в неё изменения, связанные с преобразованиями к нормализованным экранным координатам).
\[ \begin{pmatrix} z_n & 0 & 0 & 0 \\ 0 & z_n & 0 & 0 \\ 0 & 0 & z_n & 0 \\ 0 & 0 & -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} P_x \\ P_y \\ P_z \\ 1 \end{pmatrix} = \begin{pmatrix} P_x z_n \\ P_y z_n \\ P_z z_n \\ -P_z \end{pmatrix} \]
При переводе из однородных координат получим координаты проекции \(P'\):
\[ \begin{pmatrix} P_x \frac{z_n}{-P_z} \\ P_y \frac{z_n}{-P_z} \\ z_n \frac{P_z}{-P_z} = -z_n \end{pmatrix} \]
Осталось только преобразовать координаты проекции \(P'\) так, чтобы они лежали в интервале: \(\lbrack -1 \mathrel{{.}\,{.}} 1 \rbrack\). Как видно на рисунках плоскостей YZ и XZ, \(P'x\) находится в интервале \(\lbrack -w \mathrel{{.}\,{.}} w \rbrack\), \(P'y\) — в интервале \(\lbrack -h \mathrel{{.}\,{.}} h \rbrack\), а \(P_z\) – а интервале \(\lbrack -z_n \mathrel{{.}\,{.}} -z_f \rbrack\) (все точки, координаты которых выходят за границы данных интервалов, будут иметь нормализованные координаты либо большие 1, либо меньшие -1, а значит будут отброшены при рендеринге).
Начнём с \(P'y\). Для начала вычислим величину \(h\): \(\frac{h}{z_n} = \tan\left(\frac{fovy}{2}\right)\), отсюда \(h = z_n \tan\left(\frac{fovy}{2}\right)\).
Далее найдём линейные преобразования, которые необходимо совершить с \(P'y\) для перевода в интервал \(\lbrack -1 \mathrel{{.}\,{.}} 1 \rbrack\).
\[ \begin{cases} k_y h + b_y = 1 \\ k_y \left(-h\right) + b_y = -1 \end{cases} \]
Складываем оба уравнения и получаем: \(2b_y = 0\), отсюда \(b_y = 0\). Система уравнений теперь выглядит так:
\[ \begin{cases} k_y h = 1 \\ -k_y h = -1 \end{cases} \]
Отсюда получаем, что \(k_y = \frac{1}{h} = \frac{1}{z_n \tan\left(\frac{fovy}{2}\right)}\).
Проводим аналогичные преобразования для перевода \(P'_x\) в нормализованные координаты и получаем: \(b_x = 0\) и \(k_x = \frac{1}{w}\). Осталось только вычислить \(w\). Высота плоскости проецирования равна \(h\), для вычисления ширины у нас есть параметр \(aspect = \frac{width}{height}\), равный отношению ширины к высоте. Отсюда находим \(w = h \cdot aspect\) и \(k_x = \frac{1}{z_n \tan\left(\frac{fovy}{2}\right) aspect}\).
Нормальзованные координаты \(P'_{xn}\) и \(P'_{yn}\) равны:
\(P'_{xn} = P'_x \frac{z_n}{-P_z} \cdot \frac{1}{z_n \tan\left(\frac{fovy}{2}\right) aspect} = P'_x \frac{1}{-P_z} \cdot \frac{1}{\tan\left(\frac{fovy}{2}\right) aspect}\).
\(P'_{yn} = P'_y \frac{z_n}{-P_z} \cdot \frac{1}{z_n \tan\left(\frac{fovy}{2}\right)} = P'_y \frac{1}{-P_z} \cdot \frac{1}{\tan\left(\frac{fovy}{2}\right)}\)
Выразим то же самое в матричном виде:
\[ \begin{pmatrix} \frac{1}{\tan\left(\frac{fovy}{2}\right) aspect} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan\left(\frac{fovy}{2}\right)} & 0 & 0 \\ 0 & 0 & k_z & b_z \\ 0 & 0 & -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} P_x \\ P_y \\ P_z \\ 1 \end{pmatrix} \]
Осталось только найти коэффициенты \(k_z\) и \(b_z\) для преобразования \(P_z\) в нормализованные координаты. В случае, если \(P_z = -z_n\), нормализованная координата должна быть равна \(P_{zn} = -1\). Если же \(P_z = -z_f\), нормализованная координата должна быть равна \(P_{zn} = 1\). Решим систему уравнений и найдём коэффициенты \(k_z\) и \(b_z\).
\[ \begin{cases} \frac{k_z \left(-z_n\right) + b_z}{z_n} = -1 \\ \frac{k_z \left(-z_f\right) + b_z}{z_f} = 1 \end{cases} \]
Мы делим на \(z_n\) первое уравнение и на \(z_f\) второе, потому что в четвёртой компоненте \(w\) итоговой точки будет находится значение \(-P_z\), которое в первом уравнении равно \(z_n\), а во втором соответственно — \(z_f\).
Выразим \(b_z\) через первое уравнение и подставим во второе:
\[ \begin{cases} b_z = k_z z_n - z_n \\ k_z \left(-z_f\right) + k_z z_n - z_n = -z_n \end{cases} \]
Отсюда находим \(k_z\):
\[ \begin{align} k_z \left(-z_f\right) + k_z z_n - z_n & = -z_n \\ k_z \left(z_n - z_f\right) & = z_f + z_n \\ k_z & = - \frac{z_f + z_n}{z_f - z_n} \end{align} \]
Далее находим \(b_z\):
\[ \begin{align} b_z & = -\frac{z_f + z_n}{z_f - z_n} z_n - z_n \\ b_z & = \frac{-z_f z_n - z_n^2 - z_f z_n + z_n^2}{z_f - z_n} \\ b_z & = -\frac{2 z_f z_n}{z_f - z_n} \end{align} \]
Получаем, что \(P'_{zn} = \frac{-\frac{z_f + z_n}{z_f - z_n}P_z - \frac{2 z_f z_n}{z_f - z_n}}{-P_z}\). Важно помнить, что полученная нормализованная координата \(P'_{zn}\) будет использоваться только в z буфере, при растеризации она будет отброшена, так как экран является плоскостью.
Теперь нам известны все проекционные преобразования:
\[ \begin{align} P'_{xn} & = P'_x \frac{1}{-P_z} \cdot \frac{1}{\tan\left(\frac{fovy}{2}\right) aspect} \\ P'_{yn} & = P'_y \frac{1}{-P_z} \cdot \frac{1}{\tan\left(\frac{fovy}{2}\right)} \\ P'_{zn} & = \frac{-\frac{z_f + z_n}{z_f - z_n}P_z - \frac{2 z_f z_n}{z_f - z_n}}{-P_z} \end{align} \]
Осталось только выразить их в матричной форме:
\[ \begin{pmatrix} \frac{1}{\tan\left(\frac{fovy}{2}\right) aspect} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan\left(\frac{fovy}{2}\right)} & 0 & 0 \\ 0 & 0 & -\frac{z_f + z_n}{z_f - z_n} & -\frac{2 z_f z_n}{z_f - z_n} \\ 0 & 0 & -1 & 0 \\ \end{pmatrix} \cdot \begin{pmatrix} P_x \\ P_y \\ P_z \\ 1 \end{pmatrix} \]